Feasible Trajectory Planning
This is our final project for RBE550(CD-term 2023, Motion Planning @ WPI). The class focused mostly on discrete search algorithms but our team evaluated both discrete and continuous approaches for planning motions for robots with non-holonomic constraints. I focused on the discrete planning. Team size: 4.
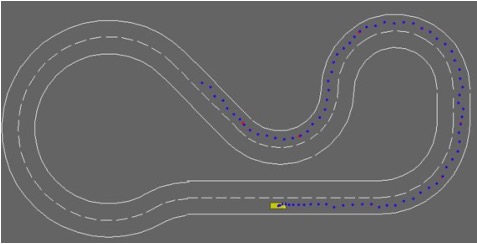
For discrete planning, we used a modified version of a simple bicycle model kinematics to represent a car. Simple grid search planning in the XY position states may not be feasible, however, you can find feasible paths if you use a grid search algorithm with node extensions based on shooting based approaches. As can be seen on the right (which is all the nodes expanded after 10 minutes), this is very inefficient if you use Dijkstra.
To speed up, we assume energy and time-based cost function and develop a heuristic based on the cost function and minimum estimated distances from the road network. We estimate the minimum distance between points on the road given a segmented road network. We use this cost function and the minimum distance between the node and target node to calculate the minimum cost in O(1), which acts as our heuristic.

Finally, since this heuristic is admissible, we can use A* on the bigger graph and find optimal discrete paths in seconds. For more details, proofs, and other assumptions, see our report's sections on the discrete method.